Harmonics in Music
We all hear harmonics in music, but many musicians avoid the study of anything that could prove that their technical “left brain” mind actually works. I’m here to tell you not to worry, you can still be an artist while learning some facts about the components of sound. Harmonics are also referred to as harmonic overtones or the overtone series.
A Brief Description of Harmonics
A tonal sound wave is made up of its fundamental frequency and harmonic frequencies. The frequency (Hz) being the number of vibrations per second. The harmonic frequencies are multiplies of the fundamental. This is because vibrating objects always create harmonics, as well as their fundamental frequency of vibration. A pure sine wave with only one frequency can exist in electronics, however, when it is sent to a loudspeaker, the speaker will vibrate with harmonics. Below is the example of a vibration of 110Hz (A2) and harmonics 2 to 12:
110 | 220 | 330 | 440 | 550 | 660 | 770 | 880 | 990 | 1100 | 1210 | 1320
Example: The Fourth Harmonic of E2 (Octave)
The fourth harmonic is isolated in the Harmonic Equalizer. The mix between the harmonic and the original signal is adjusted as this sample plays:
Are Harmonics Always Exact Multiples?
For many instruments, yes, they are. However, some have an element of inharmonicity, meaning that there is a deviation in the harmonics, away from the exact multiple of the fundamental. The classic example being the piano. The stiffness of piano wire (and hammer motion), results in inharmonicity, which is why pianos are more difficult to tune than some other instruments. Each key must be tuned so that it resonates with the harmonics of lower keys. For example, C5 must be tuned to the second harmonic of middle C (C4), even if this varies from the standard frequency of C5 (523.25Hz).
Timbre
The foremost interest in harmonics for most people is their effect on timbre. This is because it is very apparent without paying direct attention to them. For example, a clarinet sounds different to a trumpet, in part, because they have different harmonic spectra. The relative levels of their harmonics are different. The timbre of an instrument comes from the harmonic levels, as well as noise components. If you can manipulate the harmonics, you can manipulate the timbre of the instrument.
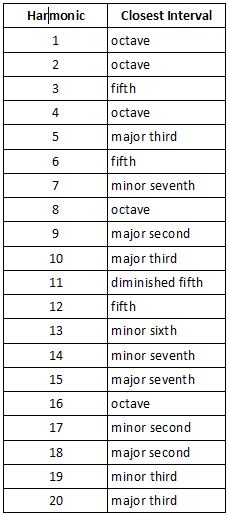
Harmonics as Musical Intervals
Here are where the intervals lie, using C1 as an example:

So we can think of a single note as a chord with these intervals within the audio. If you listen carefully to your instrument, you will be able to hear some of these notes as overtones. You will find that your particular instrument produces certain harmonics that can be heard more easily. You will also realize that certain harmonics and combinations are naturally easier to hear due to the frequency response of your ear. The response and resonant frequencies are the same for everyone with normal hearing.
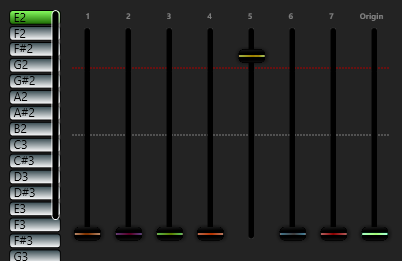
More Examples
The 5th harmonic of E2 (major third with a deviation of -14 cents)
The 7th harmonic (minor seventh with a deviation of -31 cents)
The 11th Harmonic (diminished 5th with a deviation of -49 cents)
Harmonics in Composition
Now that we know the intervals present in harmonics, we can think about composing music using these harmonic note frequencies. Audio filters can be used to bring out these harmonics.
Some harmonics lie close to (or exactly on) notes in equal temperament. The deviation, in cents, is shown in the diagram above. If your aim is to create a composition that is consonant and very tonal, the choice of harmonics would be the 2nd, 3rd, 4th, 6th, 8th, 9th, 12th, 16th, 17th, 18th, 19th and other higher ones. Some of these being octaves. If you are going for something more unusual and atonal, you will include the 5th, 7th,10th, 11th, 13th, 14th, 15th, and 20th. Particularly, the 7th, 11th, 13th, and 14th, with a deviation of 31, 49, 41, and 31 cents respectively.
Interesting compositions can be made using harmonics with deviations from equal temperament because we can employ notes that sound “off” in some ways. However, we know these frequencies do belong in the audio and would always be present. Since there is a wide range of frequencies available in the harmonics, we can create counterpoint between higher harmonics of lower notes and lower harmonics of higher notes.
Experiment with composing using harmonics and see what sounds you can create!